
《數據的假象》一書由卡爾.伯格斯特姆(Carl T. Bergstrom)及杰文.威斯特(Jevin D. West)兩位華盛頓大學教授所撰寫的,他們運用統計與生物學領域的專精知識和經驗,以生動幽默的方式,拆解取樣偏誤與數據資料數位化混淆視聽的案例,由此檢視我們的生活多麼容易受到各類數據假象的影響。
從第177期開始,《看》雜誌編輯部與多家出版社合作,為讀者精選好書,經授權後以小篇文章形式,供讀者吸收好書精華。以下內容摘自原書。

書名:數據的假象:數據識讀是深度偽造時代最重要的思辨素養,聰明決策不被操弄
作者:卡爾‧伯格斯特姆(Carl T. Bergstrom)、杰文‧威斯特(Jevin D. West)
譯者:穆思婕、沈聿德
出版社:天下雜誌出版
類別:思考邏輯、統計、數據分析
出版日期:2022年6月1日
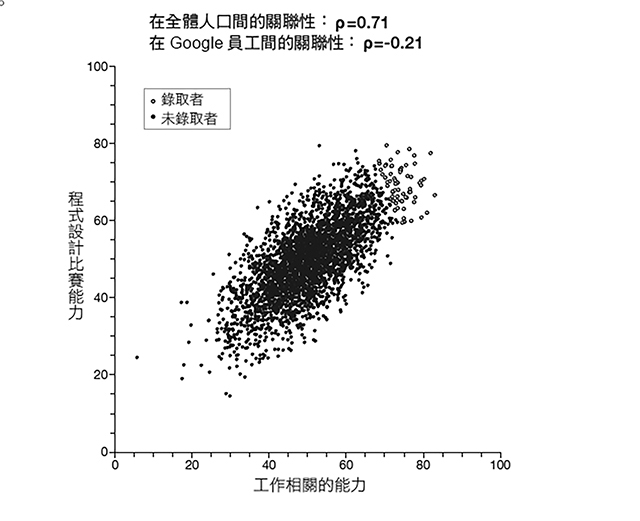
五年前,Google的工程師們在自己公司的招聘過程中應用機器學習技術,希望找到最具生產力的未來員工,結果卻讓他們大感意外:個人的工作績效表現,與其先前參加程式設計比賽的優異成就,呈現負相關。原因可能是擅長程式設計比賽的人具備某種特質,成不了理想員工。Google的研發長彼得.諾維克(Peter Norvig)推測,或許贏得程式設計比賽的人習慣快速解決問題,不過工作時速度放慢則成效較佳。然而我們倒不該過快妄下結論,程式設計比賽成績和工作績效表現之間的負相關,反而可能是取樣使然,這些員工並非從大範圍人口中隨機取樣而得,這些人是因為Google側重其程式設計與其他能力始獲青睞。話說回來,想理解負相關是如何產生的,就得先回到一個更多人感興趣的問題上:為什麼帥哥都是渾球?
數學家喬丹‧艾倫伯格(Jordan Ellenberg)曾提出一個名為「柏格森矛盾」(Berkson's Paradox)的現象,藉以解釋某個經常耳聞的抱怨。我們那些還在約會市場尋尋覓覓的朋友,偶爾會埋怨自己和某個帥哥出去約會後才發覺對方是渾球,但每次碰到好人卻都不是帥哥。失望之餘,我們通常如此解釋:外表具吸引力的人,因為被捧得老高、是相當受歡迎的擇偶對象,所以有當渾球的條件。不過,還有另一個可能的解釋。
▲圖1
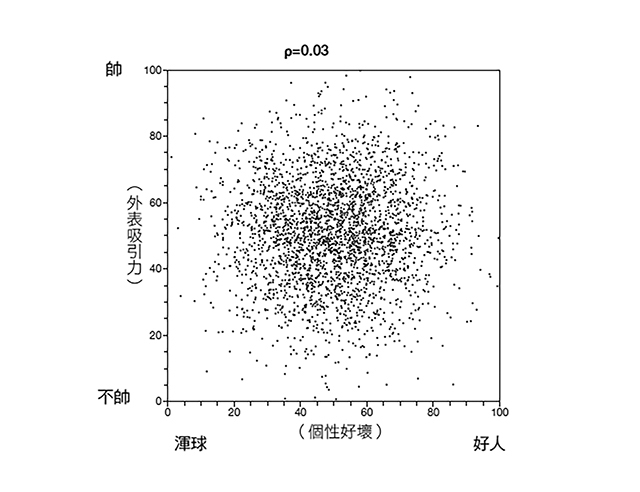
艾倫伯格要我們在一個二維圖上標註出自己想要的伴侶,其中,水平軸代表他們個性好壞,縱軸則代表他們外表優劣。我們可以從圖1看到大家所做的結果分布。
在這個圖裡,外表吸引力和個性好壞基本上互不相關。相較於非帥哥,帥哥是渾球的可能性沒有比較高或低。到目前為止,我們沒有理由認為個性好的男生較不帥,或帥哥個性較不好。
▲圖2
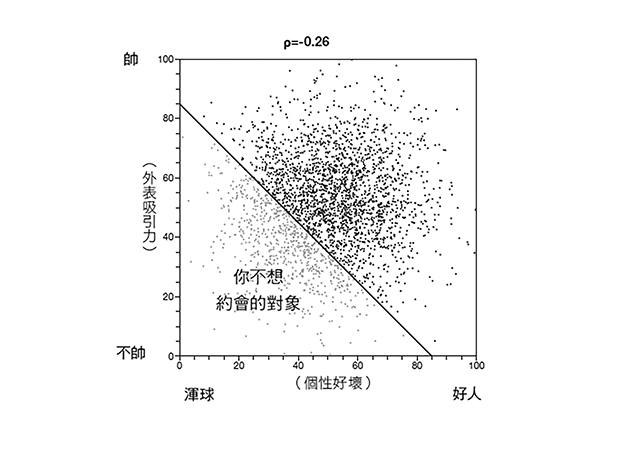
現在來看看當條件變成你願意約會的對象時,情況有何不同。大家肯定都不想跟外表不帥的渾球約會。不過,我們可能會因為對方個性極佳而願意忍受其外表不足之處,反之亦然。因此,在這個二維圖(圖2)裡,你願意約會的對象會落在對角線以上的區域。
這下子,在你願意約會的對象當中,外表吸引力和個性好壞之間出現適度的負相關。比起你願意約會的對象,一個真的很帥且個性又好的可能性就比較低,另一方面,一個人真的個性很好且外表又帥的可能性也比較低。
這就是「柏格森矛盾」發揮作用。在我們出於個人所好,想挑個性又想挑外表的同時,便已經在自己願意約會的對象之間,造就出個性和外表吸引力呈現負相關的現象。
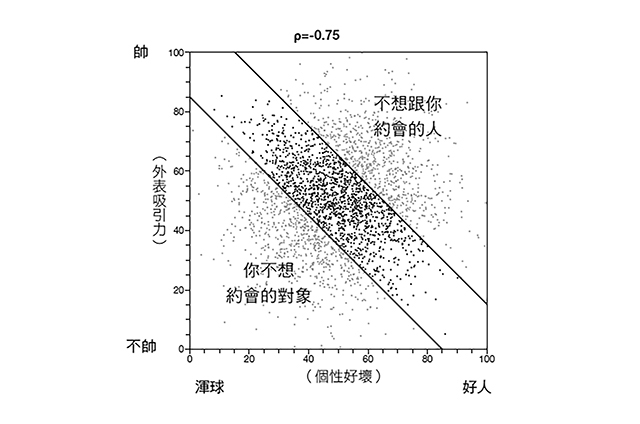
另一個類似的過程則反此道而行。不只我們在挑願意約會的對象,我們也是別人挑選的對象。除非你是獲獎無數的創作型歌手約翰‧傳奇(John Legend),否則一定有人捨你不選。這麼一來,你可能的約會對象中又要去掉一類。
▲圖3
那剩下的是誰呢?你可能的約會對象僅落於可能伴侶圖(圖3)中狹長的對角帶區域。在這此一對角區域裡,外表吸引力跟個性好壞之間呈現強烈負相關。儘管人口大致沒有出現負趨勢,但是,這兩個彼此獨立、在我們願意約會的對象與願意和我們約會的對象上出現的「柏格森矛盾」,卻早已創造出可能伴侶間的負相關現象。
▲圖4
讓我們回頭來看,程式設計比賽獲勝能力與工作績效表現之間的負相關。在一般人身上,我們大有理由可以這兩者間呈現強烈的正相關。儘管美國大多數的員工完全不懂程式設計,可是程式設計能力是能在Google擔任工程師的先決條件之一。該公司的人才招募經理人,真的會用程式設計比賽裡設定的那些任務或難題,做為評選方式。或許這種招募過程對程式設計比賽能力稍嫌重視,卻犧牲做事有效的特質。果真如此,最後就有可能得到比賽能力與工作績效表現為負相關的結果。圖解說明如圖4。
一旦你開始思考「柏格森矛盾」,就會發現它無處不在。為什麼美國職棒大聯盟的最佳野手們往往打擊表現都普普通通,而最佳打擊手往往守備表現差強人意?這是因為打擊守備皆表現平庸的棒球員很多,但這些人根本沒機會登上大聯盟舞台。如果你玩桌遊《龍與地下城》(Dungeons & Dragons)的話,為何你的最佳戰士領導力卻如此薄弱,而最佳術士還不堪一擊?答案是因為每新晉一級要分配額外能力點數時就得在不同能力之間取捨的緣故。
就連在公開狀況下取樣所得的統計結果,也可能與你我預期相反。假設學校可以根據學生的等第積分平均(Grade Point Averages,GPAs)提名學生角逐全國性的獎學金。我們等提名公布後檢視200位獲得提名的學生,結果發現獲得提名的女學生們等第積分平均為3.84,男同學們的平均則為3.72。這個樣本當中的學生人數龐大,以致於無法將分數差異單純歸咎於機率使然。我們能不能由此斷定學校偏好提名男學生,即使其等第積分平均較低也無妨?乍看之下好像如此。如果學校提名男女學生的標準一樣,為什麼兩者的等第積分平均沒有大致相同呢?
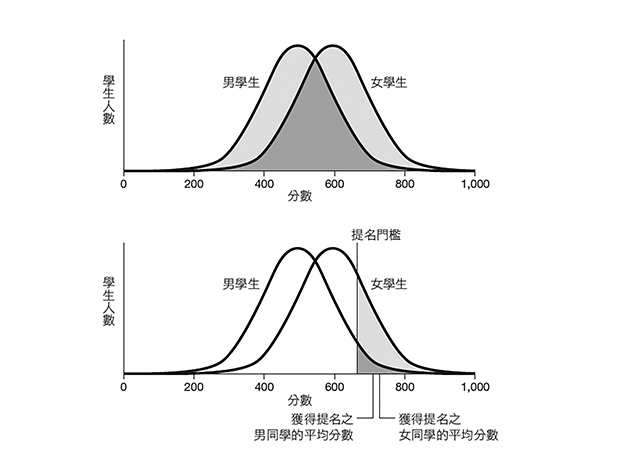
▲圖5
其中一個可能的解釋是男女學生各別的等第積分平均分布有所不同。果真如此,即使套用相同的提名門檻挑出成績最好的學生,這些獲得提名的男女學生各別的等第積分平均分布依然會有所不同。在圖5裡,成績最好的女學生們得分都極高,而成績最好的男學生們得分只跨過門檻一些,如此使得得分達標的學生平均分數有所不同。
雖然這不完全是「柏格森矛盾」,但重點是取樣可能出現各種有趣的結果。我們試圖理解出自於數據資料的型樣(Pattern)時,值得先想想其中有無任何取樣偏誤或刻意的取樣操弄,如果有的話,那些因素又會如何影響你所觀察到的型樣。
(以上節選自《數據的假象》第6章〈取樣偏誤〉第149頁~第160頁)







